Differential equations Questions and Answers
Math
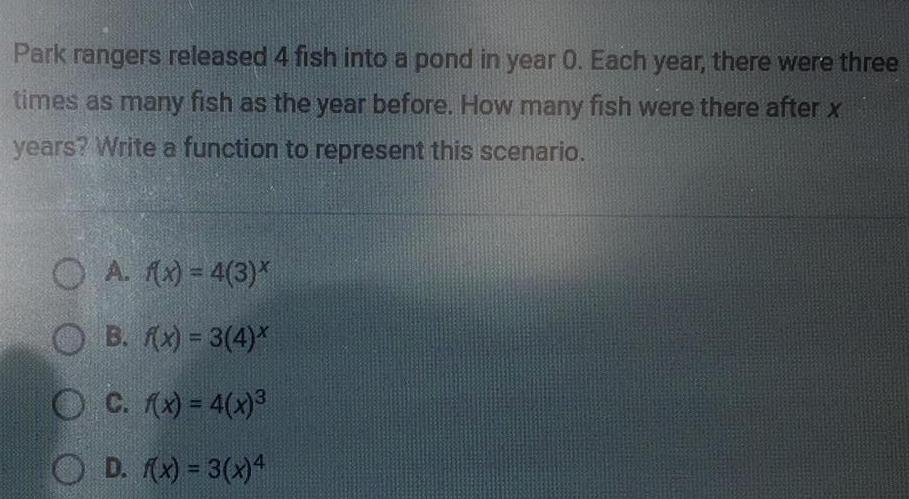
Differential equationsPark rangers released 4 fish into a pond in year 0 Each year there were three times as many fish as the year before How many fish were there after x years Write a function to represent this scenario A f x 4 3 OB f x 3 4 OC f x 4 x D f x 3 x 4

Math
Differential equationsThe function y 100e 0 045t models the amount y of radioactive material remaining in grams as a function of time t in days Calculate the half life of this radioactive material Round your answer to the nearest tenth 1 A B I NE
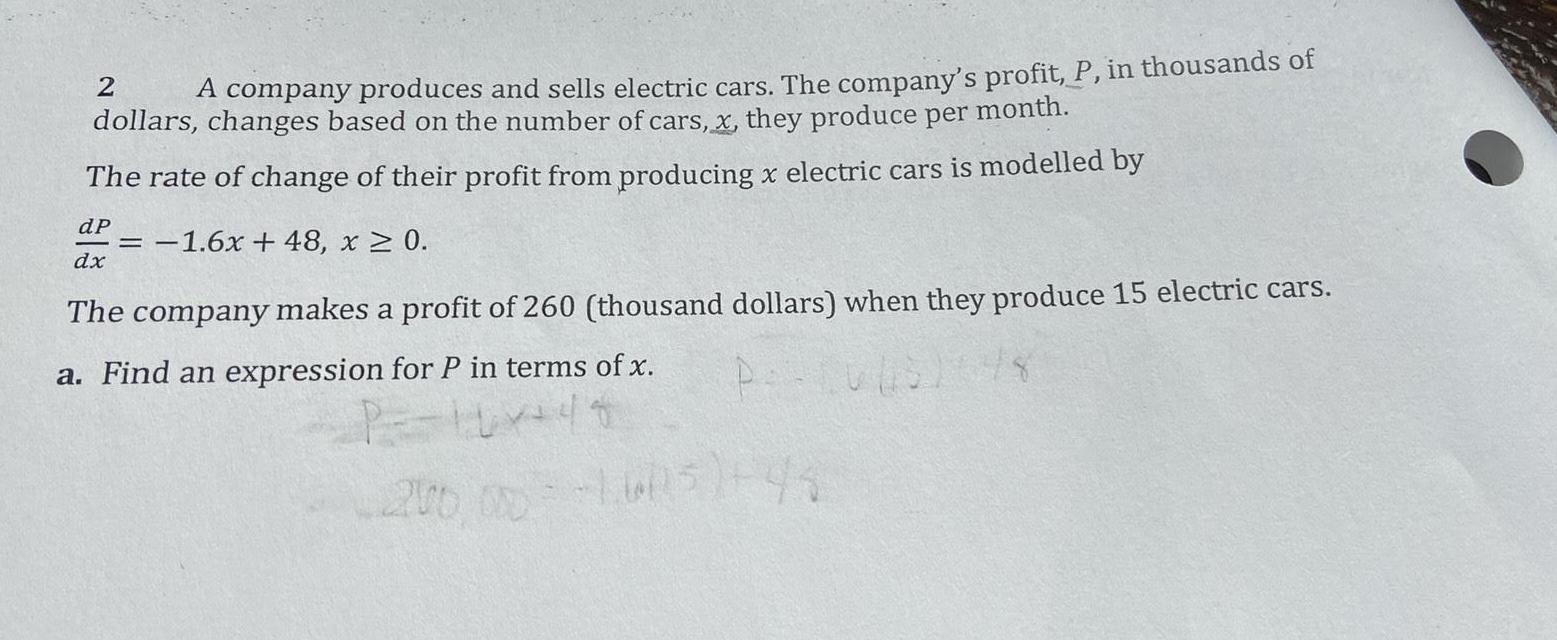
Math
Differential equations2 A company produces and sells electric cars The company s profit P in thousands of dollars changes based on the number of cars x they produce per month The rate of change of their profit from producing x electric cars is modelled by dP 1 6x 48 x 0 dx The company makes a profit of 260 thousand dollars when they produce 15 electric cars a Find an expression for P in terms of x P P 10 441 200 000 1605 43

Math
Differential equationsA coolant is injected into engine fluid causing the temperature of the engine fluid to decrease with respect to time at a rate that is proportional to the difference of the fluid s instantaneous temperature T and the fluid s original temperature To Select the differential equation that represents the relationship 10 points OdT c T T dt dt c T T T t T To T t To T
Math
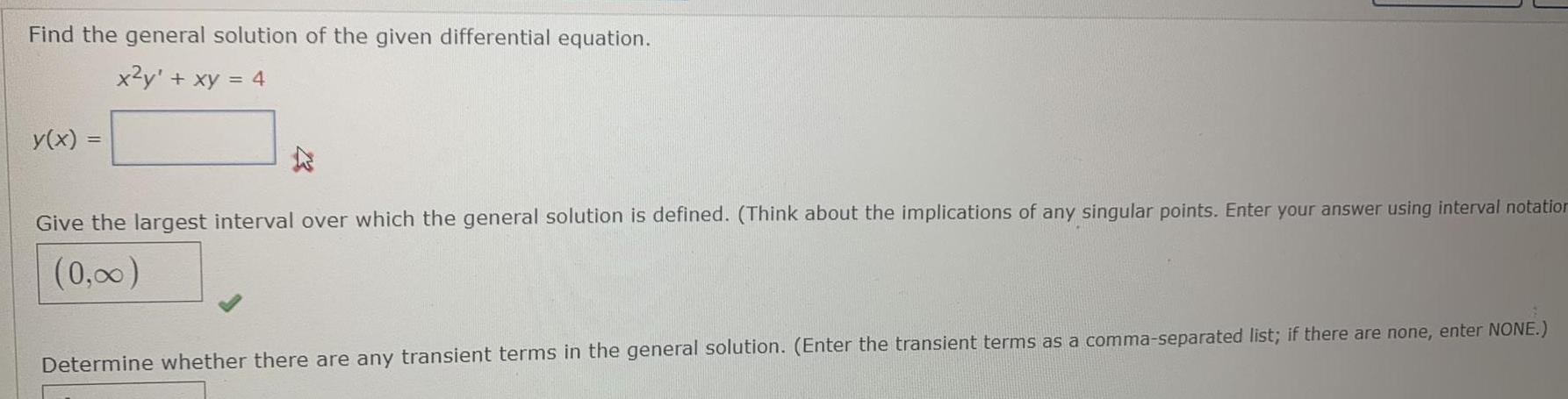
Differential equationsFind the general solution of the given differential equation.
x²y + xy = 4
Give the largest interval over which the general solution is defined. (Think about the implications of any singular points. Enter your answer using interval notation)
Determine whether there are any transient terms in the general solution. (Enter the transient terms as a comma-separated list; if there are none, enter NONE.)
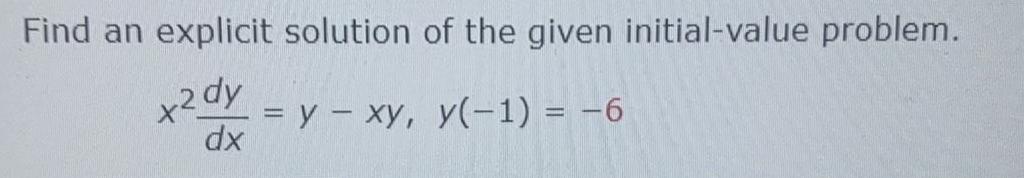
Math
Differential equationsFind an explicit solution of the given initial-value problem.
x2dy/dx = y-xy, y(-1) = -6

Math
Differential equationsConsider the following differential equation and seek a power series solu-
tion centered at ro = 0.
(x²+4)y" - xy + 5y = 0
By putting the equation in standard form, we can see that the radius of
convergence is at least
(A) 2
(B) 4
(C) 5
(D) 6

Math
Differential equationsFind the first four nonzero terms in a power series expansion about x=0 for the solution to the given initial value problem.
w" +5xw'-w=0; w(0)=4, w'(0) = 0

Math
Differential equationsUse implicit differentiation to find the tangent line of the function In(y) = x ln(x) at the point (2,4).
Math
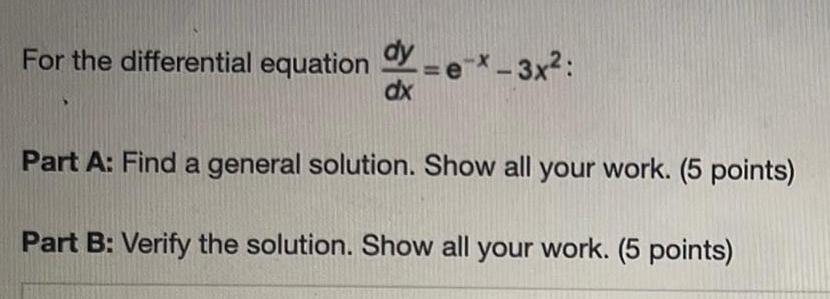
Differential equationsFor the differential equation dy/dx =e-x-3x²:
Part A: Find a general solution. Show all your work.
Part B: Verify the solution. Show all your work.

Math
Differential equationsIf f(x) = 2² +1, use the limit definition of the derivative to compute f'(z). You can use derivative rules to check your answer, but answers calculated without using the definition of derivative will receive very little credit.

Math
Differential equationsSolve the initial value problem x'(t) = Ax(1) for 120, with x(0)=(3,1) Classify the nature of the origin as an attractor, repeller, or saddle point of the dynamical system described by x¹=Ax. Find the directions of greatest attraction and/or repulsion
2 -4
6-8

Math
Differential equations5. Consider differential equation
dy/dx + (2/x) y = xy³, y(1) = 1/2
Find y(10) numerically using the following methods and h = 0.5, 0.25, 0.125 and calculate
the errors in each case. You have to use MATLAB for this problem. (10 Points each)
a. Forward Euler's method
b. Backward Euler's method
c. Modified Euler's method
d. Improved Euler's method
e. Fourth-Order Runge Kutta Method

Math
Differential equationsA jogger runs around a circular track of radius 65 ft. Let (x, y) be her coordinates, where the origin is the center of the track. When the jogger's coordinates are (39, 52), her x-coordinate is changing at a rate of 16 ft/s. Find dy/dt.
dyldt = ft/s

Math
Differential equationsThe rate of change of the number of raccoons N(t) in a population is directly proportional to 380 N(t), where t is the time in years. When t = 0, the population is 120, and when t = 4, the population has increased to 160. Find the population when t = 8.
(Round your answer to the nearest integer.)
raccoons

Math
Differential equationsGiven the sets of system linear of differential equation;
2x"+6x'+y" + 3y' = 12e ^-t
x'+2x + y' = 0
(a) Determine x(t) by using Elimination Method.
(b) Determine y(t).
(c) Check number of arbitrary constant and determine the final solutions.

Math
Differential equationsIn drawing the slope field for the differential equation dy/dx= x+3y-4, I would draw a short line segment for different points on the x-y plane.
What slope should I draw the line segment at the point (0,-2)?
Your Answer:

Math
Differential equationsSolve the differential equation, such that the equation passes through the given point (x, y). (Remember to use absolute values where appropriate.)
dy/dx = 5/x (1, 2)
y = log(x5) +2

Math
Differential equationsConsider the autonomous first-order differential equation dy/dx = y - y³ and the initial condition y(0) = y₀. Sketch the graph of a typical solution y(x) when y₀, has the
given values.
(a) y₀ > 1
Math
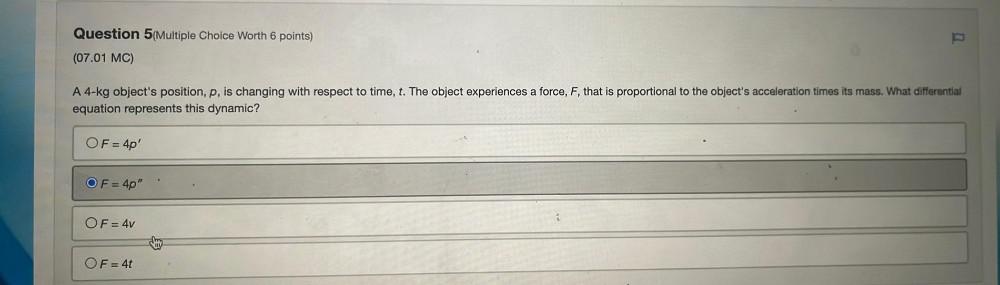
Differential equationsA 4-kg object's position, p, is changing with respect to time, t. The object experiences a force, F, that is proportional to the object's acceleration times its mass. What differential equation represents this dynamic?
A. F = 4p'
B. F = 4p"
C. F = 4v
D. F = 4t

Math
Differential equationsThe differential equation y' = 3x will produce which of the following?
A. A slope field with parallel tangents along the diagonal
B. A slope field that does not have rows or columns of parallel tangents
C. A slope field with columns of parallel tangents
D. A slope field with rows of parallel tangents
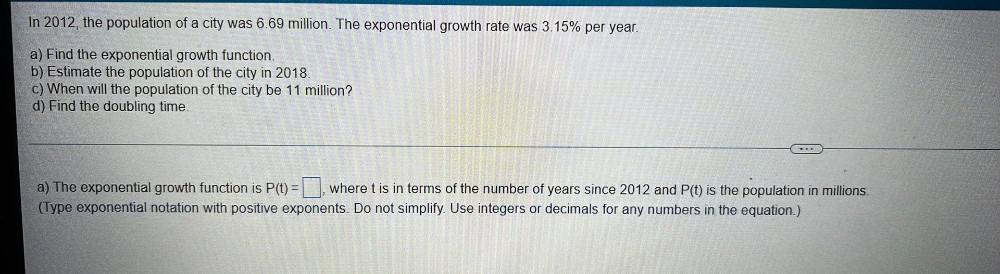
Math
Differential equationsIn 2012, the population of a city was 6.69 million. The exponential growth rate was 3.15% per year.
a) Find the exponential growth function.
b) Estimate the population of the city in 2018.
c) When will the population of the city be 11 million?
d) Find the doubling time.
a) The exponential growth function is P(t) = ▢ where t is in terms of the number of years since 2012 and P(t) is the population in millions.
(Type exponential notation with positive exponents. Do not simplify. Use integers or decimals for any numbers in the equation.)
Math
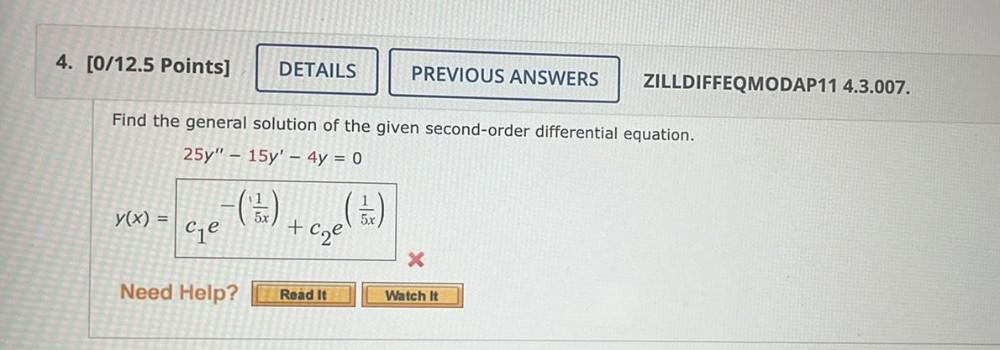
Differential equationsFind the general solution of the given second-order differential equation.
25y" – 15y' - 4y = 0
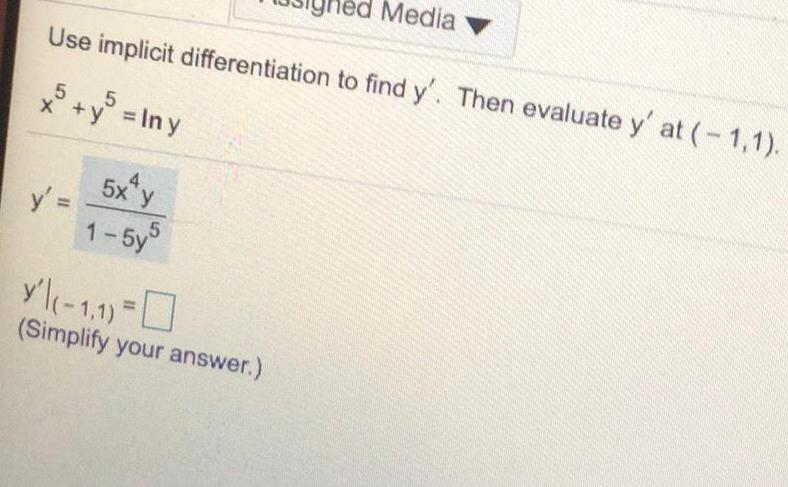
Math
Differential equationsUse implicit differentiation to find y'. Then evaluate y' at (-1,1).
x^5 + y^5 = lny
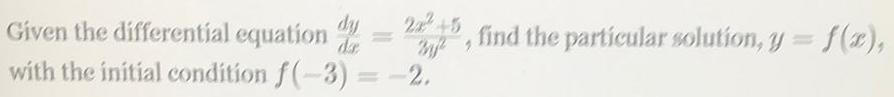
Math
Differential equationsGiven the differential equation dy/dx = 2x^2+5/3y^2, find the particular solution, y = f(x), with the initial condition f(-3) = -2.

Math
Differential equationsFirst find f' and then find f.
f"(x) = 6x³ + 10x² + 3x +3,
f'(1) = -1,
f(1) = -9.
f'(x) =
f(x) =
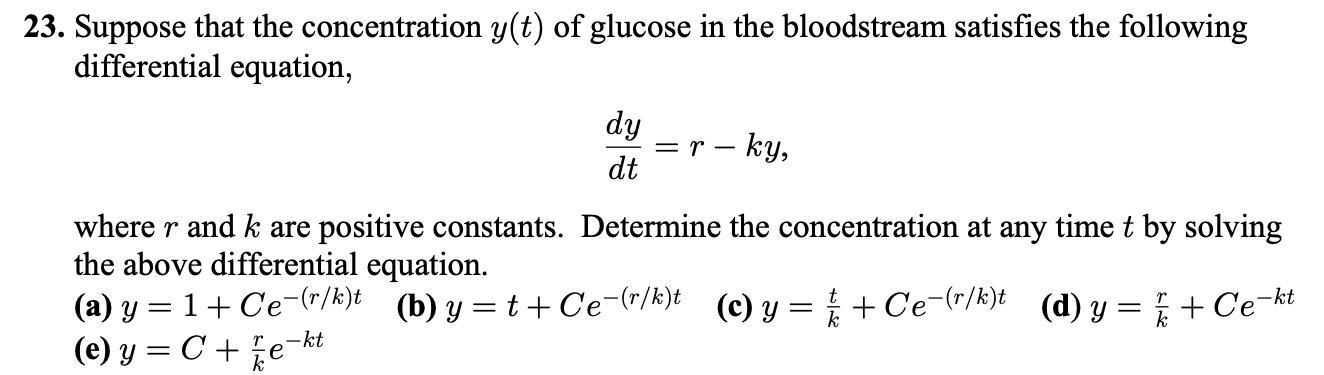
Math
Differential equationsSuppose that the concentration y(t) of glucose in the bloodstream satisfies the following
differential equation,
dy/dt =r-ky,
where r and k are positive constants. Determine the concentration at any time t by solving
the above differential equation.
(a) y = 1+ Ce(r/k)t (b) y=t+Ce-(r/k)t (c) y = // + Ce(r/k)t (d) y = / + Ce-kt
(e) y = C + e-kt
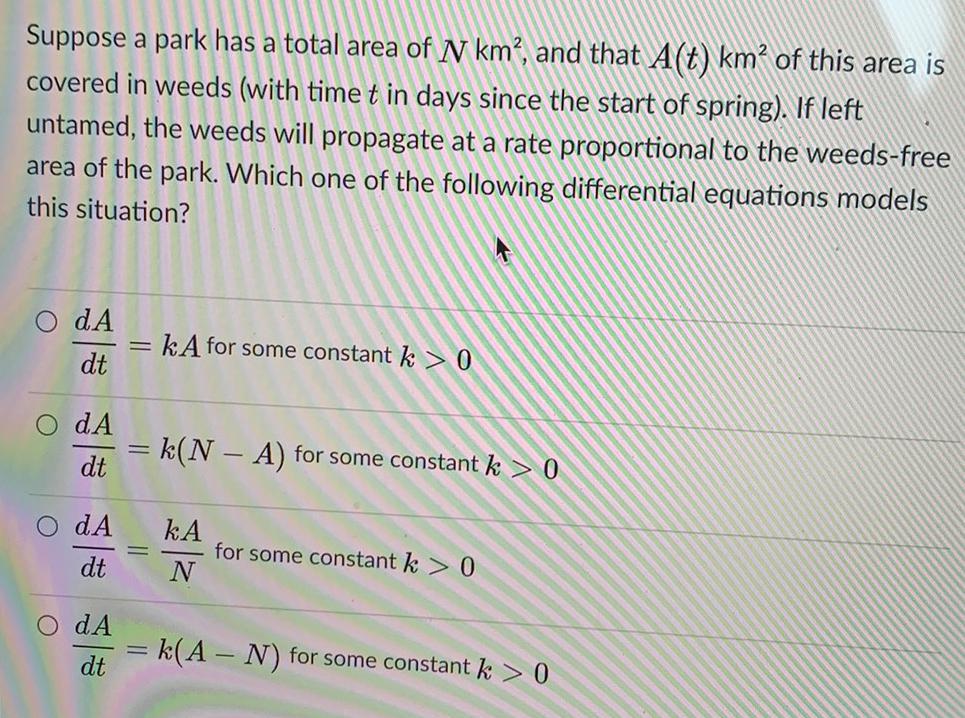
Math
Differential equationsSuppose a park has a total area of N km², and that A(t) km² of this area is
covered in weeds (with time t in days since the start of spring). If left
untamed, the weeds will propagate at a rate proportional to the weeds-free
area of the park. Which one of the following differential equations models
this situation?

Math
Differential equationsSome medicines can wear off in the body exponentially. In this case, assume the rate decays hourly for a starting amount of 250 mg of medication according to the equation:
M = 300(0.84)t
Solve this equation to determine the number of hours, t, that it will take for the initial 300 mg of medicine to decrease to 10 mg. Round to two decimal places.

Math
Differential equationsMonthly sales of a Jeep Wrangler are expected to increase at a rate of
S' (t) = -24t3 Jeep Wrangler per month, where t is time in months and S(t)
is the number of Jeep Wranglers sold each month. The Company that makes the Jeep
Wrangler plans to stop making them when monthly sales reach 300 Jeep Wranglers.
If monthly sales now (t-0) are 1200 Jeep Wranglers, find S(t). How long will the
company continue to manufacture this model?
Math
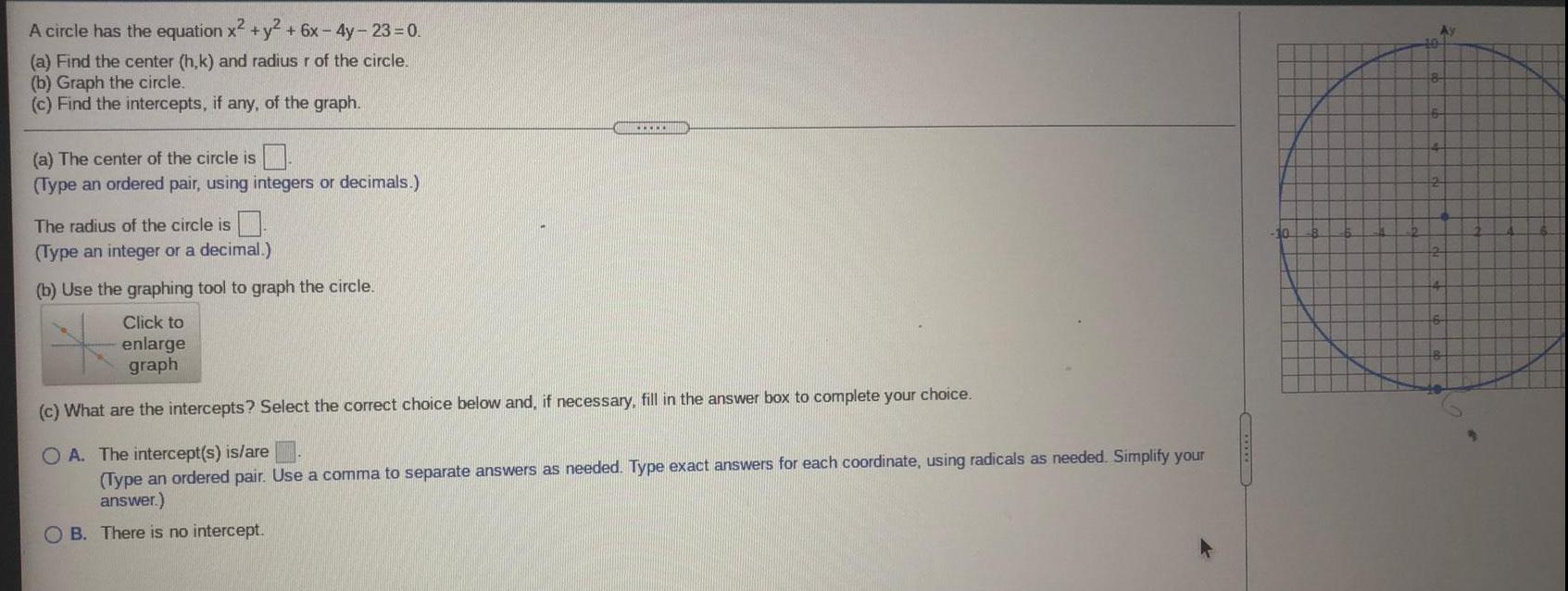
Differential equationsA circle has the equation x2 + y² + 6x-4y-23=0.
(a) Find the center (h,k) and radius r of the circle.
(b) Graph the circle.
(c) Find the intercepts, if any, of the graph.
(a) The center of the circle is
(Type an ordered pair, using integers or decimals.)
The radius of the circle is
(Type an integer or a decimal.)
(b) Use the graphing tool to graph the circle.
(c) What are the intercepts? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The intercept(s) is/are
(Type an ordered pair. Use a comma to separate answers as needed. Type exact answers for each coordinate, using radicals as needed. Simplify your
answer.)
B. There is no intercept.

Math
Differential equationsA spherical iron ball 12 in. in diameter is coated with a layer of ice of uniform thickness. If the ice melts at a rate of 10 in /min, how fast is the thickness of the ice decreasing when it is 3 in. thick? How fast is the outer surface area of ice decreasing?

Math
Differential equationsA thermometer reading 24° Celsius is placed in an oven preheated to a constant temperature. Through a glass window in the oven door, an observer records that the thermometer read 32° after 35 seconds and 37° after 70 seconds. How hot is the oven?
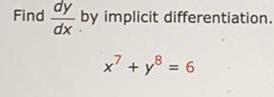

Math
Differential equationsA closed box is constructed of 4200 cm² of cardboard. The box is a cuboid, with height h cm and square base of side x cm. What is the value of x which maximises the volume of the box? Give your answer in cm correct to 3 significant figures.

Math
Differential equationsFirst find the general solution (involving a constant C) for the given differential equation. Then find the particular solution that satisfies the indicated condition.
ds /dt = 11t²+5t-5;s-76 at t=0
The general solution is s=

Math
Differential equationsPark rangers released 4 fish into a pond in year 0. Each year, there were three
times as many fish as the year before. How many fish were there after x
years? Write a function to represent this scenario.
A. f(x) = 4(3)*
B. f(x) = 3(4)*
C. f(x) = 4(x)³
D. f(x) = 3(x)4

Math
Differential equationsUsing our quadratic equation
knowledge match the following scenarios.
1. Hitting a golf ball on the moon
2. Hitting a golf ball on Earth from the
top of a tall building
3. Hitting a baseball on Jupiter
4.
Hitting a baseball on Earth by a
bionic man
5. Hitting a baseball on Earth by a 10
foot tall person
A. h(x) = -16x² +500x+4
B. h(x) = -50x² +50x+4
C. h(x) = -8x² +100x
D. h(x) = -16x² +75x+8
E. h(x) = -16x² +150x+300
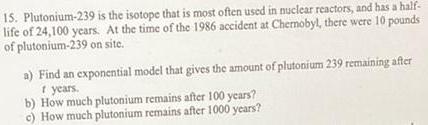
Math
Differential equations15. Plutonium-239 is the isotope that is most often used in nuclear reactors, and has a half-
life of 24,100 years. At the time of the 1986 accident at Chernobyl, there were 10 pounds
of plutonium-239 on site.
a) Find an exponential model that gives the amount of plutonium 239 remaining after
t years.
b) How much plutonium remains after 100 years?
c) How much plutonium remains after 1000 years?

Math
Differential equationsSolve the following initial value problem. By this we mean that you should find y = y(x) which satisfies both equations below. (See the linked
example.)
2
=
13/03 +5x², _y(1) = −19
x⁹
ANSWER: y(x) =
dy
dx
M

Math
Differential equationsThe radioactive element carbon-14 has a half-life of 5750 years. A scientist determined that the bones from a mastodon had lost 51.3% of their carbon-14. How old were the bones at the
time they were discovered?
The bones were about years old.
(Round to the nearest integer as needed.)
CHUCKCLLNINGS

Math
Differential equationsWhen a cake is removed from an oven, its temperature is measured at 300°F. Three minutes later its temperature is 200°F.
i. Find the temperature T(t) of the cake after t minutes assuming the room temperature is 30°F.
ii. How long will it take for the cake to cool off to 40°F? [Assume Newton's law of cooling/

Math
Differential equationsUse Euler's Method to make a table of values for the approximate solution of the differential equation with the specified initial value. Use n steps of size h. (Round your answers to six decimal places.)
y' = 6x - 3y, y(0) = 5, n = 10, h = 0.05
![Determine A, B, and C so that y = A cosh (Ca) + B sinh (Cx) satisfies the conditions yn - 9y = 0, y(0) = 1, y' (0) = 3. Take C > 0.
a) [A = 4, B = 1/3, C = 3]
b) [A = 1, B = 1, C = 3]
c) [A = 1, B = 2, C = 3]
d) [A = 2, B = 1, C = 1]
e) [A = 3, B = 1, C = 1]](https://media.kunduz.com/media/sug-question/raw/58102418-1657714092.3925958.jpeg?w=256)
Math
Differential equationsDetermine A, B, and C so that y = A cosh (Ca) + B sinh (Cx) satisfies the conditions yn - 9y = 0, y(0) = 1, y' (0) = 3. Take C > 0.
a) [A = 4, B = 1/3, C = 3]
b) [A = 1, B = 1, C = 3]
c) [A = 1, B = 2, C = 3]
d) [A = 2, B = 1, C = 1]
e) [A = 3, B = 1, C = 1]

Math
Differential equationsFind the equilibrium solution of the following equation, make a sketch of the direction field, for t20, and determine whether the equilibrium solution is stable.
y' (t) = -(y/2)-4
The equilibrium solution is y=

Math
Differential equationsVerify that the general solution satisfies the differential equation. Then find the particular solution that satisfies the initial condition(s).
y = Ce-12x
y' +12y = 0
y = 24 when x = 0

Math
Differential equationsWrite and find the general solution of the differential equation that models the verbal statement. (Use k for the constant of
proportionality. Use C for the constant of integration.)
The rate of change of Q with respect to x is inversely proportional to the square of x.
dx
||
11
kx²
2
kx³
3
+ C
X
X
Math
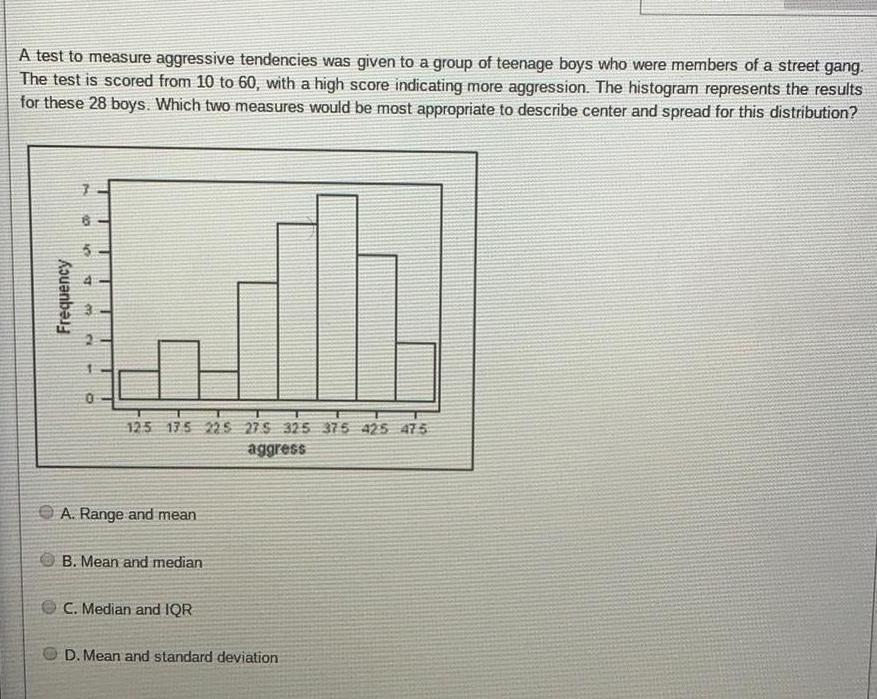
Differential equationsA test to measure aggressive tendencies was given to a group of teenage boys who were members of a street gang. The test is scored from 10 to 60, with a high score indicating more aggression. The histogram represents the results for these 28 boys. Which two measures would be most appropriate to describe center and spread for this distribution?
A. Range and mean
B. Mean and median
C. Median and IQR
D. Mean and standard deviation

Math
Differential equationsThe half-life of the radioactive element plutonium-239 is 25,000 years. If 16 grams of plutonium-239 are initially present, how many grams are present after: (round your answer to the nearest hundredth) Find the exponential model first.
a. 25,000 years
b. 50,000 years
c. 75,000 years
d. 100,000 years
e. 125,000 years
Math
Differential equationsDetermine whether the following equation is separable. If so, solve the given initial value problem.
sect (y' (t)) = 1, y(0) = 6
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution to the initial value problem is y=
B. The equation is not separable.